一个小需求

最近刚在项目中接触到一个类似业务流水号（订单号）的生成唯一性编号的需求，这个东西之前倒是没接触过，在很久以前遇到的最多也就拿数据库生成自增序列完事，而流水号一般需要其中的数据有意义，并可反推等。

找到代码中生成流水号的工具类准备学习参考一番，看到了一些类似如下的代码：

byte[] byteArray = new byte[4];
byteArray[0] = (byte)(intNum >>> 24);
byteArray[1] = (byte)(intNum >>> 16);
byteArray[2] = (byte)(intNum >>> 8);
byteArray[3] = (byte)(intNum);
return byteArray;

由于对 2 进制、位运算一直是学习远大于使用，所以一时愣住没反应过来这里是做的什么操作，只是知道在一个 byte 数组中各拿出几位来分别存储一些业务字段就是生成流水号的关键。

在学习研究了一番后，恍然大悟，原来高精度数值用 byte 数组来存储是这样实现的（啊，后知后觉）。

下文均以一个正数转 byte 数组举例。

如何用 byte 数组存储高精度数值

高精度类型直接强转低精度时，会以低精度的位数为主，忽略高精度数据的其余高位，所以只用一个 byte 是不够的。

以一个 int 类型的数值为例，一个 int 有 4 字节，这就要用一个长度为 4 的 byte 数组来存储。

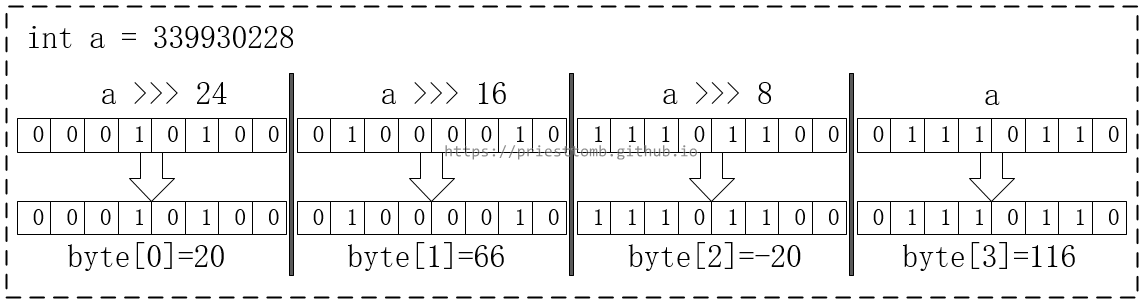
将 int 中每 8 bit 都转成一个 byte，再形成数组，就能得到一个存储着 int 的 byte 数组。

使用 >>> 运算符，就能快速得到 int 数值中的每个 8 bit，而要把这 4 个 byte “拼”回 int 型数值时，又需要注意其中负数的问题（参考补码的说明《关于2的补码》）。

如果直接使用左移+与运算，会是这样：

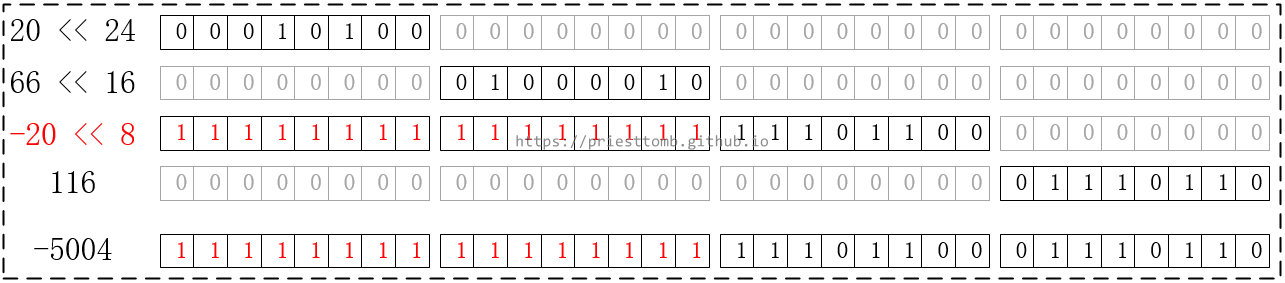
结果当然是错的，要把负数“转正”，用 & 0xff 把高位补 0 ，代码如下：

public static int byteToInt(byte[] byteArray) {
	int intNum = (byteArray[0] & 0xff) << 24
			| (byteArray[1] & 0xff) << 16
			| (byteArray[2] & 0xff) << 8
			| (byteArray[3] & 0xff);
	return intNum;
}

小端序与大端序

在需求中，看到了大端序和小端序这个字眼，感觉上一次看到（也可能没看到）这两个词可能是在大学时期的课堂上，于是再查了一下，权当巩固了。

刚才的示例中，把 int 数据的最高位（即左移 24 位得到的那 1 个字节）存到了 byte 数组最小的第 0 位，而最低位（即末尾的那 1 个字节）存到了 byte 数组最大的第 3 位，这种顺序就是字节的大端序。

大端序某种程度上来说，更符合大多数人类的感官，比如列出一个数组来，下标小的在左边，下标大的在右边，而刚好从左到右存的是数据的高位到低位，一目了然。

小端序与大端序相反，把数据的高位字节放在数组的最后，而低位字节放到第 0 位，比如上面的 int 值 339930228 用小端序存储，则是 [116, -20, 66, 20] 。

关于字节顺序，也只是了解这么一个概念，更详细的可以参考《理解字节序》、《字节顺序》。

最后

每每都会感慨，如果不是在真实的需求中为了解决一个问题而去学习了解一个东西，大概率还是学了就忘。。结合需求、多深入了解，才会记得久一点（吧。。